Brauer-Manin obstructions requiring arbitrarily many classes
Jen Berg
March 2, 2023
The results in this talk are joint work with Carlo Pagano, Bjorn Poonen, Michael Stoll, Nicholas Triantafillou, Bianca Viray, and Isabel Vogt.
This project started at the Park City Mathematics Institute (PCMI) 2022 program on Number Theory Informed by Computation
To read up on some of the background on obstructions to rational points relevant to this work, a fantastic resource is Bianca's notes from her PCMI lectures.
Obstructions to rational points
an overview
Obstruction Sets
Given a nice variety $X$ over a number field $k$, there is no known general method to decide whether $X(k)$ is nonempty. But don't despair!
Instead, we build an obstruction set $S$ such that
- $\, X(k) \subset S$
- $\, S$ is computable (hopefully)
When $S = \emptyset$, this guarantees $X(k) = \emptyset$ and we say that $S$ obstructs the existence of $k$-rational points on $X$.
Local obstructions
Given a place $v$ of $k$, a first obstruction set comes from the embedding $k \hookrightarrow k_v. \,$ If $X(k_v) = \emptyset\,$ then this forces $X(k) = \emptyset$.
For proper $X$, we package together all local information into a single set $X(\mathbb{A}_k) = \prod_v X(k_v).$ It is a finite, effective computation to determine whether $X(\mathbb{A}_k) \ne \emptyset$.
A class of varieties $\mathcal{C}$ satisfies the local-to-global principle if for each $X \in \mathcal{C}$ $$\underbrace{X(\mathbb{A}_k) \ne \emptyset}_{\text{local points exist}} \implies \underbrace{X(k) \ne \emptyset}_{\text{global points do too!}}$$
Refined obstructions
While there are classes of varieties that do satisfy the local-to-global principle (e.g. quadric hypersurfaces by Hasse-Minkowski or Severi-Brauer varieties), many more do not.
So we need a refinement of our local obstructions in general, i.e., an obstruction set $S$ such that $$\Large X(k) \subset \, S \subset \, X(\mathbb{A}_k)$$
One such obstruction set is called the Brauer-Manin set $X(\mathbb{A}_k)^{\text{Br}}$ and is defined using the Brauer group of $X$.
The Brauer Group
Many perspectives
The Brauer Group (via examples)
Let's start with some examples.
$\text{Br}(\mathbb{C}) = 0 \qquad \text{Br}(\mathbb{R}) = \mathbb{Z}/2\mathbb{Z} \qquad \text{Br}(\mathbb{F_q}) = 0$
When $F$ is a field, the Brauer group, $\text{Br}(F)$, gives a rough measure of the complexity of Galois theory of $F$. Gives insight into how prevalent norm elements are.
e.g., only Galois extension of $\mathbb{R}$ is $\mathbb{C}$ and $a \in \mathbb{R}$ is a norm iff $a > 0$.
The Brauer Group (cohomological perspective)
When $F$ is a field, $\text{Br}\, F \cong H^2(\text{Gal}(F^\text{sep}/F), (F^\text{sep})^\times)$.
The Brauer group of a scheme $X$ is defined in terms of étale cohomology, $\text{Br}\,X := H^2_{\text{\'et}}(X, \mathbb{G}_m)$. We recover $\text{Br}\, F = \text{Br}\, \text{Spec} \, F$.
The Brauer group is functorial: if there is a morphism of varieties $f \colon X \to Y$ then there is a homomorphism $f^\ast \colon \text{Br}\, Y \to \text{Br}\, X$.
The Brauer Group (algebraic perspective)
For $F$ a field, $\text{Br} \, F$ is also defined in terms of central simple algebras up to Brauer equivalence. It is a torsion abelian group under tensor product, where the identity element is the class of $M_n(F)$.
EXAMPLE: Let $a, b \in F^\times$. The quaternion algebra $(a,b)_F$ is element of order dividing $2$ in $\text{Br}\, F$ defined by the $4$ dimensional $F$-algebra \[ F \oplus F\, i \oplus F \, j \oplus F \, ij, \quad i^2 = a, \, j^2 = b, \, ij = - ji, \]
The algebra $(a,b)_F$ is trivial in $\text{Br}\, F$ $\iff$ the conic $ax^2 + by^2 = z^2$ has an $F$-rational point $\iff$ $a \in N(F(\sqrt{b})^\times)$
The Brauer Group (geometric perspective)
$\textrm{Br}(F) = \{ Y : Y_{\overline{F}} \simeq \mathbb{P}^n_{\overline{F}} \}/\simeq_{\tiny F} \qquad $ ($F$ a field)
The $2$-torsion is generated by classes of conics.
$\textrm{Br}\,\mathbf{k}(X) = \{ Y : Y_{\overline{\mathbf{k}(X)}} \simeq \mathbb{P}^n_{\overline{\mathbf{k}(X)}} \}/\simeq_{\tiny F} \qquad $ ($X$ nice variety)
GOOD NEWS: When $X$ is smooth, $\,\text{Br}(X) \subset \text{Br}\,\mathbf{k}(X)$ is a subgroup and there is a concrete way to detect exactly which elements in $\text{Br}\,\mathbf{k}(X)$ belong to $\text{Br}\,X$ (so called everywhere unramified elements)
Deep breaths
The Brauer group is a multi-faceted object that captures useful arithmetic and geometric information.
However, the point is not to overwhelm you, but instead to show that there are many ways to think about it! Depending on context, one may be more helpful than another.
We still need the Brauer group to define an obstruction set (that was our goal!!)
Defining the Brauer-Manin obstruction
Fundamental exact sequence
Let $k$ be a number field. For each place $v$ of $k$, there is an injective homomorphism $$ \text{inv}_v \colon \text{Br}\, k_v \to \mathbb{Q}/\mathbb{Z}, $$ that is an isomorphism for non-archimedean $v$. Furthermore, these isomorphisms fit together into a short exact sequence
$$\begin{CD} 0 @>> > \text{Br}\, k @>> > \bigoplus_v\, \text{Br} \, k_v @>\sum_v \text{inv}_v >> \mathbb{Q}/\mathbb{Z} @>> > 0 \end{CD} $$
The Brauer-Manin pairing
For each extension $F/k$ the functoriality of the Brauer group gives a pairing $$ \begin{align*} \text{Br}\, X \times X(F) &\to \text{Br}\, F \\ (\alpha, x) \quad &\mapsto \langle \alpha, x \rangle := x^\ast \alpha \end{align*}$$ where we view a point $x \in X(F)$ as a map $\, x \colon \text{Spec}\, F \to X$
For each extension $k_v/k$ the functoriality of the Brauer group gives a pairing $$ \begin{align*} \text{Br}\, X \times X(k_v) &\to \text{Br}\, k_v \\ (\alpha, x) \quad &\mapsto \langle \alpha, x \rangle := x^\ast \alpha \end{align*}$$ where we view a point $x \in X(k_v)$ as a map $\, x \colon \text{Spec}\, k_v \to X$
Since $X$ is proper, we have $X(\mathbb{A}_k) = \prod_v X(k_v)$, so we can apply the pairings componentwise to get a pairing
Putting it all together
So, we get a commutative diagram
$$\begin{CD} @. \text{Br}\, X \times X(k)@>>> \text{Br}\, X \times X(\mathbb{A}_k)@.\\ @. @VVV @VVV\\ @. \text{Br}\,k @>>> \oplus_v \text{Br}\,k_v @. @. @. \end{CD}$$
$$\begin{CD} @. \text{Br}\, X \times X(k) @>>> \text{Br}\, X \times X(\mathbb{A}_k) @.\\ @. @VVV @VVV\\ 0 @>>> \text{Br}\,k @>>> \oplus_v \text{Br}\,k_v @>{\sum_v \text{inv}_v}>> \mathbb{Q}/\mathbb{Z} @>>>0 \end{CD}$$
Since the bottom row is a complex, the induced map $\small X(k) \times \text{Br}\, X \to \mathbb{Q}/\mathbb{Z}$ is identically 0. So, for all $\small \alpha \in \text{Br}\, X$, we have
$$ X(k) \subset X(\mathbb{A}_k)^\alpha := \{(x_v) \in X(\mathbb{A}_k) : \textstyle \langle \alpha, (x_v) \rangle = 0\}.$$
Finally an obstruction set
Taking the intersection of $\small X(\mathbb{A})^\alpha$ for all $\small \alpha$, we obtain the Brauer-Manin set
$$ X(\mathbb{A}_k)^{\text{Br}} := \left\{(x_v) \in X(\mathbb{A}_k) : \langle \alpha, (x_v) \rangle = 0 \, \, \text{for all $\alpha \in \text{Br}\, X$} \right\} $$
When $X(\mathbb{A}_k) \ne \emptyset$ but $X(\mathbb{A}_k)^{\text{Br}} = \emptyset$, we say $X$ has a Brauer-Manin obstruction to the local-to-global principle.
Useful properties
The constant classes in $\small \text{Br}\, X$ are the subgroup $\small \text{Br}_0\,X := \text{im}(\pi^\ast \colon \text{Br}\,k \to \text{Br}\, X)$, where $X \xrightarrow{\pi} \text{Spec} \, k$ is the structure morphism.
The Brauer-Manin set depends only on the quotient $\text{Br}\,X/ \text{Br}_0\,X$.
- Constant algebras give no obstruction: For any $\alpha_0 \in \text{Br}_0 \, X$, we have $X(\mathbb{A_k})^{\alpha_0} = X(\mathbb{A}_k)$.
- Obstruction from a subgroup determined by the generators: If $\alpha, \beta \in \text{Br}\, X$, then $X(\mathbb{A}_k)^\alpha \cap X(\mathbb{A}_k)^\beta = \bigcap_{\gamma \in \{ \alpha^i \beta^j \mid i,j \in \mathbb{Z}\}} X(\mathbb{A}_k)^{\gamma}$
So you've defined an obstruction, now what?
Using the Brauer group, we defined the Brauer-Manin set $$X(k) \subset X(\mathbb{A}_k)^{\text{Br}} \subset X(\mathbb{A}_k).$$ But how useful is this in practice for detecting information about $X(k)$?
Practicalities
We set out to construct an obstruction set that's actually computable.
BAD NEWS: There's no general effectivity result for computing the Brauer-Manin set nor is there an approach known to work in full generality.
GOOD NEWS: There are still many examples where we can compute whether there is a Brauer-Manin obstruction!
Provided we have a good enough understanding of the geometry of $X$ (e.g., the structure of $\small \text{Pic}(\overline{X})$ as a Galois-module), we can often compute the structure of $\small \text{Br}\, X/ \text{Br}_0 \, X$.
Computing the Brauer-Manin set
Today we'll focus on examples where we can determine $\small \text{Br}\, X/ \text{Br}_0 \, X$. But even with this, we still have to compute the obstruction set it cuts out.
Thankfully, given $\small \alpha \in \text{Br}\, X$ there are theoretical results that make life easier.
The evaluation maps are locally constant: $ \small \langle \alpha, - \rangle \colon X(k_v) \to \mathbb{Q}/\mathbb{Z}$ is locally constant. For many nice varieties, the evaluation maps are in fact constant for all but finitely many places.
Examples can be misleading
In nearly all examples in the literature where we have $X(\mathbb{A}_k)^{\{ \alpha_i \}} = \emptyset$, in fact $ \small \langle \alpha_i, - \rangle \colon X(k_v) \to \mathbb{Q}/\mathbb{Z}$ is constant for all $i$ and for all $v$. But these examples were specifically built to have these properties in order to get an obstruction!
However, we really should expect to have places $v$ for which the evaluation maps are not constant. (Work of Harari and later Bright, among others, can make this statement more precise.)
Consequences: If there exists a place $v$ for which the evaluation $\small \langle \alpha, - \rangle \colon X(k_v) \to \mathbb{Q}/\mathbb{Z}$ is not constant, then $\small X(\mathbb{A}_k)^\alpha \subsetneq X(\mathbb{A}_k)$ and if the image is as large as possible then $\small X(\mathbb{A}_k)^{\alpha} \ne \emptyset.$
Can we predict anything in advance?
Thankfully, one can show that if $X$ has a Brauer-Manin obstruction, then it was caused by a finite collection of Brauer classes.
Creutz and Viray introduced the following definition: Let $X$ be a nice $k$-variety. We say that $\small \mathcal{B} \subset \text{Br}\,X$ captures the Brauer-Manin obstruction if $\small X(\mathbb{A}_k)^{\text{Br}} = \emptyset \implies X(\mathbb{A}_k)^{\mathcal{B}} = \emptyset$.
So one can ask, given a class of varieties, can we describe $\mathcal{B} \subset \text{Br}\,X$ that captures the Brauer-Manin obstruction and is more easily computable?
It's complicated...
Given a class of varieties, can we describe $\mathcal{B} \subset \text{Br}\,X$ that captures the Brauer-Manin obstruction and is more easily computable?
YES: For varieties closely related to abelian varieties by work of Skorobogatov–Zarhin (2017), Creutz–Viray (2018), and Nakahara (2019)
For cubic and quartic del Pezzo surfaces, there is always a single Brauer class that captures the Brauer-Manin obstruction (Poonen, Colliot-Thélène 2000)
It's complicated...
Given a class of varieties, can we describe $\mathcal{B} \subset \text{Br}\,X$ that captures the Brauer-Manin obstruction and is more easily computable?
UNCLEAR: The situation is murkier for curves (Creutz–Viray–Voloch, 2019); in particular, their results suggest any such subgroup $\mathcal{B}$ likely depends on more than the genus and the degree.
The 2-primary subgroup does not capture the Brauer-Manin obstruction for K3 surfaces (B. and Várilly-Alvarado 2020; Gvirtz, Loughran, Nakahara 2021).
Main Results
In full generality, cannot do better quantitatively than finiteness of $\mathcal{B}$.
Theorem (BPPSTVV)
Let $k$ be a global field with $\text{char}\, k \ne 2$ and let $N \in \mathbb{Z}_{>0}$. There exists a smooth projective geometrically integral variety $Y/k\,$ s.t.
- $Y(\mathbb{A}_k)^{\text{Br}} = \emptyset$, and
- for all subgroups $B \subset \text{Br}\, Y$ with $\#B < N$, we have $Y(\mathbb{A}_k)^{B} \ne \emptyset$
How does one start to find such examples over a number field $k$?
Restricting the scope
When in search of $Y/k$ exhibiting a particular arithmetic property, helpful to focus on a class of varieties with common geometric invariants.
Geometrically rational surfaces, i.e. those birational to $\mathbb{P}^2$ over $\overline{k}$, are practical candidates for our task since
- They're birational to a del Pezzo surface or a conic bundle over $\mathbb{P}^1$
- Often straightforward to compute generators for the Brauer group
- Conjecturally, $\, Y(k) = \emptyset \implies Y(\mathbb{A}_k)^{\text{Br}} = \emptyset$
Key steps
To build our examples with an obstruction requiring subgroups of the Brauer group of a fixed size we will:
- Focus on conic bundle surfaces whose Brauer quotients we can control
- Give a helpful group theoretic reinterpretation of what it means to have a Brauer-Manin obstruction
- Describe a base change construction that realizes our group theoretic ideas
Conic bundles
A conic bundle over $\mathbb{P}^1_k$ is a smooth, projective, geometrically integral surface $X$ over $k$ equipped with a morphism $\pi \colon X \to \mathbb{P}^1_k$ whose generic fiber is a smooth conic over $\mathbf{k}(\mathbb{P}^1_k)$
Let $a \in k^\times \setminus k^{\times 2}$ and let $f(x_0, x_1) \in k[x_0, x_1]$ be a separable homogenous polynomial of even degree. We will consider a conic bundle $X_{a,f}$ which is the smooth, projective model of the affine surface \[ y^2 - a z^2 = f(x_0, 1) \]
Brauer groups of our conic bundles
$X = X_{a,f} \xrightarrow{\pi} \mathbb{P^1}$ with affine equation $y^2 - az^2 = f(x)$
Assume that the splitting field of $f$ does not contain $k(\sqrt{a})$ and that $f$ factors into the product of irreducibles, $f = \prod_{j=0}^{n} f_j$, each with even degree.
Then the quaternion algebras $\alpha_j = \pi^\ast(a, f_j) \in \text{Br}\,\mathbf{k}(X)$ generate $\text{Br}(X)/\text{Br}_0(X)$
A group theoretic interpretation
GOAL : Understand group theoretically necessary (and sufficient) conditions to achieve the requirement that a specific number of Brauer classes must all be used for an obstruction
Brauer-Manin Pairing Revisited
Recall the Brauer-Manin pairing:
$$ \begin{align*} \text{Br}(Y) \times Y(\mathbb{A}_k) &\longrightarrow \mathbb{Q}/\mathbb{Z} \\ ( \alpha,(y_v) ) &\longmapsto \langle \alpha, (y_v) \rangle := \textstyle \sum \limits_{v} \text{inv}_v (\underbrace{y_v^\ast \alpha}_{\in \, \text{Br}\,k_v}) \end{align*} $$
Let $B$ be a finite subgroup of $\text{Br}(Y)$. There is a map of sets
\[ \phi \colon Y(\mathbb{A}_k) \to \hat{B} := \text{Hom}(B, \mathbb{Q}/\mathbb{Z})\]
coming from the Brauer-Manin pairing: given $\small (y_v) \in Y(\mathbb{A}_k)$, keep track of $\small \langle \alpha, (y_v) \rangle \in \mathbb{Q}/\mathbb{Z}$ for each $\alpha \in B$.
Obstruction from a subgroup
The obstruction set $Y(\mathbb{A}_k)^B$ is nonempty precisely when there exists an adelic point $(y_v) \in Y(\mathbb{A}_k)$ such that $(y_v)$ is orthogonal to each $\alpha \in B$ under the Brauer-Manin pairing, i.e. $\small \langle \alpha, (y_v) \rangle = 0$ for all $\alpha \in B$
That is, the obstruction set is empty precisely when the $0$ map is not in the image of $\phi \colon Y(\mathbb{A}_k) \to \hat{B} = \text{Hom}(B, \mathbb{Q}/\mathbb{Z})$
A group theoretic lemma
Let $B$ be a finite subgroup of $\text{Br}(Y)$ and consider the image of $\phi \colon Y(\mathbb{A}_k) \to \hat{B} := \text{Hom}(B, \mathbb{Q}/\mathbb{Z})$
- $Y(\mathbb{A}_k)^B = \emptyset\,$ if and only if $0 \not \in \text{im}\,\phi \subset \hat{B}$
- Suppose $B \cong (\mathbb{Z}/2\mathbb{Z})^n$ for some $n \ge 1$ and gives a Brauer-Manin obstruction. Then no proper subgroup of $B$ gives an obstruction if and only if $\,\text{im}\,\phi = \hat B \setminus \{0\}$.
Illustrating the idea
Suppose $n=3$, so that $B = \langle \alpha_1, \alpha_2, \alpha_3 \rangle \cong (\mathbb{Z}/2\mathbb{Z})^3$. To get $X(\mathbb{A})^B = \empty$ but no proper subgroup causes an obstruction, we want that the points in $X(\mathbb{A}_k)$ give rise to all $\small 2^3-1$ nonzero outcomes from the Brauer-Manin pairing with the $\alpha_i$ (rows represent images of adelic points)
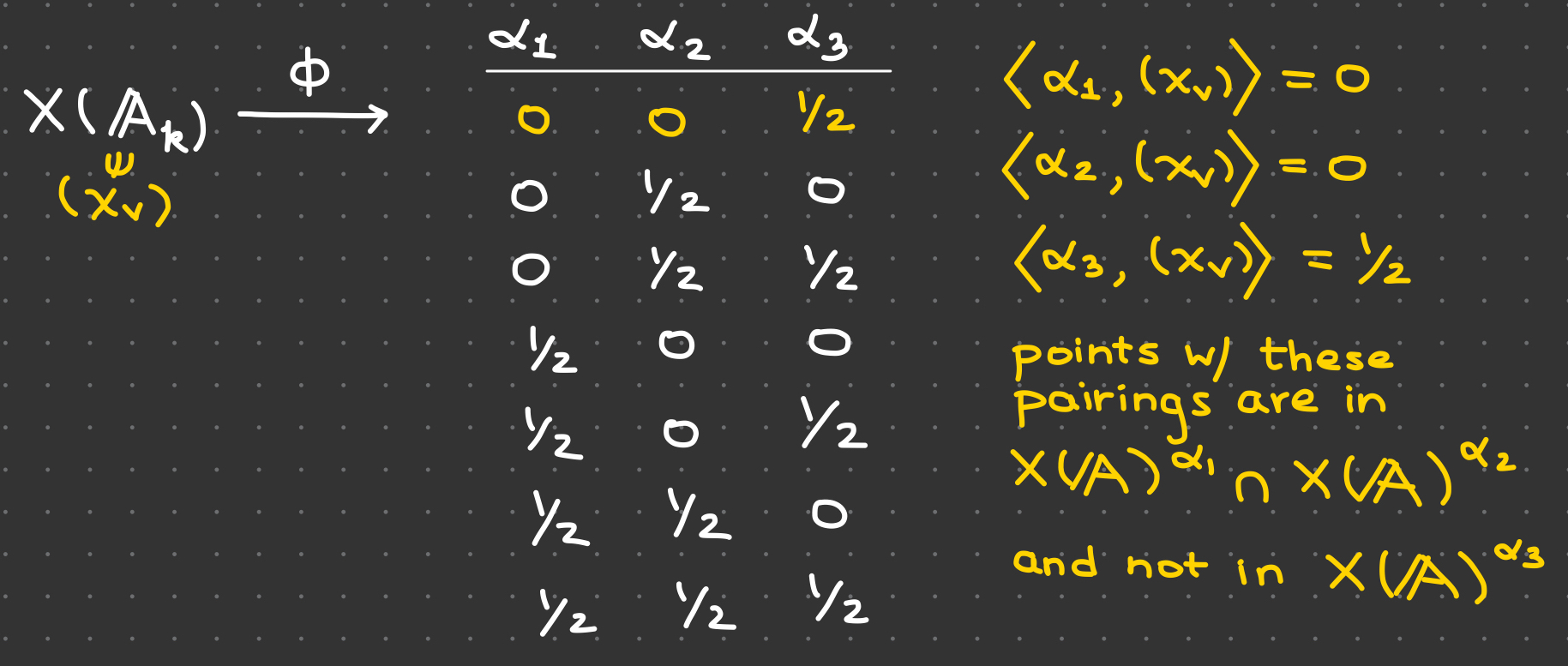
New goal
Find $Y/k$ where $\text{Br} \, Y$ contains a subgroup $B$ isomorphic to $(\mathbb{Z}/2\mathbb{Z})^n$ such that the induced map $B \to \text{Br}\, Y / \text{Br}_0\, Y$ is an isomorphism, and the image of $Y(\mathbb{A}_k)$ in $\hat{B}$ is everything except the $0$ map.
Since we can build conic bundles $X := X_{a,f}$ with Brauer groups satisfying the first property, we need only to figure out how to achieve the second.
Sum of local evaluations
Assume $B$ is fixed and set $\hat{B} = \text{Hom}(B, \mathbb{Q}/\mathbb{Z})$.
For each place $v$ of $k$, there is a map of sets $\phi_v \colon Y(k_v) \to \hat{B}$
(Take $\small y_v \in Y(k_v)$ and keep track of $\small \langle \alpha, y_v \rangle \in \mathbb{Q}/\mathbb{Z}$ for each $\alpha \in B$.)
The image is the $0$ map except for finitely many places $v$. By definition, the image of $\phi \colon Y(\mathbb{A}_k) \to \hat{B}$ is the sum of the $\text{im}\, \phi_v$.
To arrange $\text{im} \,\phi = \hat{B}\setminus \{0\}$ one option is to have $\text{im}\, \phi_{v_0} = \hat{B}\setminus \{0\}$ for a single place $v_0$ and $\text{im}\, \phi_{v} = \{0\}$ for all other places $v$.
Illustrating the idea
As noted earlier, one way to achieve this is with a single place $v_0$
| The place $v_0$ | ||
|---|---|---|
| $\alpha_1$ | \( \alpha_2 \) | \( \alpha_3 \) |
| \( 0\) | \( 0\) | \( \frac{1}{2}\) |
| \( 0\) | \( \frac{1}{2}\) | \( 0\) |
| \( 0\) | \( \frac{1}{2}\) | \( \frac{1}{2}\) |
| \( \frac{1}{2}\) | \( 0\) | \( 0\) |
| \( \frac{1}{2}\) | \( 0\) | \( \frac{1}{2} \) |
| \( \frac{1}{2}\) | \( \frac{1}{2}\) | \( 0\) |
| \( \frac{1}{2}\) | \( \frac{1}{2}\) | \( \frac{1}{2} \) |
| All other places $v \ne v_0$ | ||
|---|---|---|
| $\alpha_1$ | \( \alpha_2 \) | \( \alpha_3 \) |
| \( 0\) | \( 0\) | \( 0\) |
Illustrating the idea (multiple places)
| $ \substack{\normalsize X(k_{v_0}) \\ \textcolor{blue}{x_{v_0} \in}} \xrightarrow{\phi_{v_0}}$ |
|---|
| The place $v_0$ | ||
|---|---|---|
| $\alpha_1$ | \( \alpha_2 \) | \( \alpha_3 \) |
| \( 0\) | \( 0\) | \( 0\) |
| \( \frac{1}{2}\) | \( 0\) | \( 0\) |
| $\mathbf{0}$ | \( \mathbf{\frac{1}{2}}\) | \( \mathbf{0}\) |
| \( 0\) | \( 0\) | \( \frac{1}{2}\) |
| $ \substack{\normalsize X(k_{v_1}) \\ \textcolor{blue}{x_{v_1} \in}} \xrightarrow{\phi_{v_1}}$ |
|---|
| The place $v_1$ | ||
|---|---|---|
| $\alpha_1$ | \( \alpha_2 \) | \( \alpha_3 \) |
| \( \mathbf{\frac{1}{2}} \) | \( \mathbf{\frac{1}{2}}\) | \( \mathbf{\frac{1}{2}} \) |
| \( 0 \) | \( \frac{1}{2}\) | \( \frac{1}{2}\) |
| \( \frac{1}{2}\) | \( 0\) | \( \frac{1}{2}\) |
| \( \frac{1}{2}\) | \( \frac{1}{2}\) | \( 0\) |
And $\small \text{im}\, \phi_v$ is 0 for all $\small v \ne v_0, v_1$. If we take $\small (P_v)$ so that $\small P_{v_0} = x_{v_0}$ and $\small P_{v_1} = x_{v_1}$ then $$\begin{align*} \textstyle \langle \alpha_1, (P_v) \rangle &= \textstyle \textcolor{blue}{0 + \frac{1}{2}} + 0 = \frac{1}{2} \\ \textstyle\langle \alpha_2, (P_v) \rangle &= \textstyle\textcolor{blue}{\frac{1}{2} + \frac{1}{2}} + 0 = 0 \\ \textstyle\langle \alpha_3, (P_v) \rangle &= \textstyle\textcolor{blue}{0 + \frac{1}{2}} + 0 = \frac{1}{2} \end{align*}$$
An upper bound
You might worry that we could need to check MANY places, relative to $n$. Thankfully, that's not the case.
Theorem (BPPSTVV)
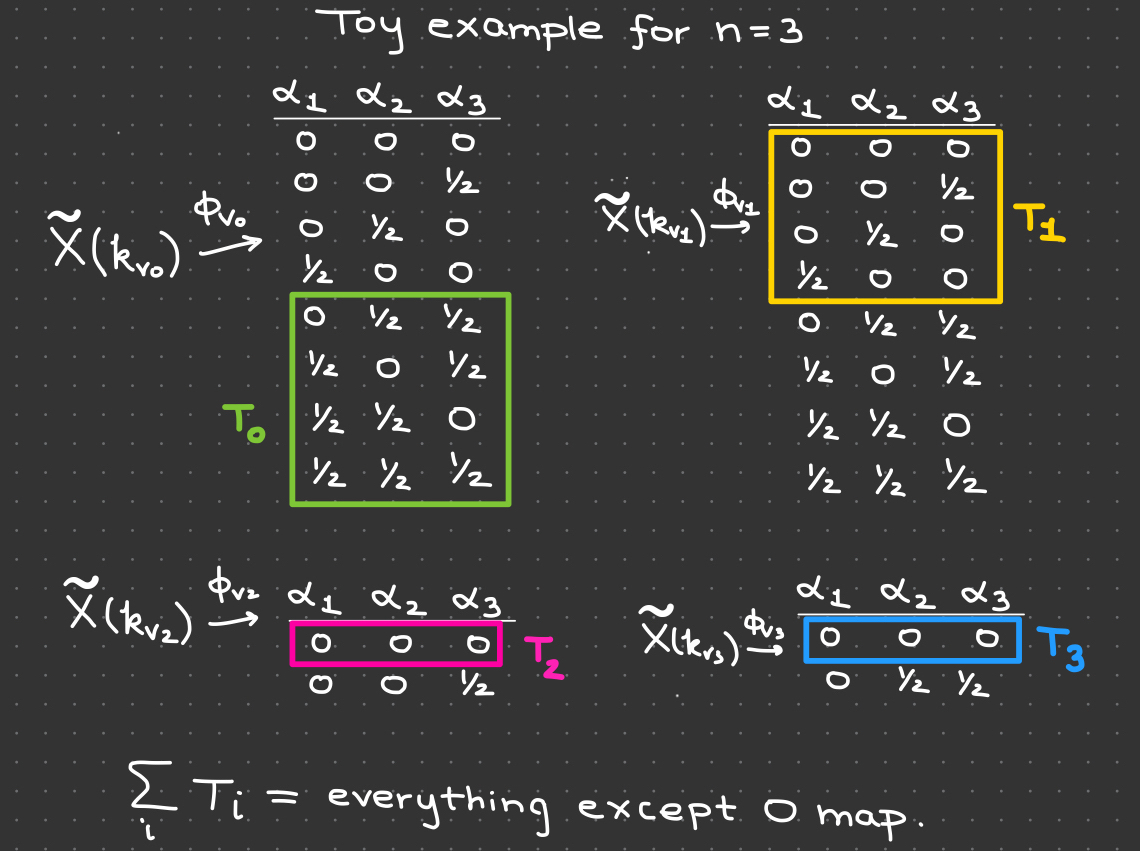
Let $B \cong (\mathbb{Z}/2\mathbb{Z})^n$ and let $T_{0}, \dots, T_{t} \subset \text{Hom}(B, \mathbb{Q}/\mathbb{Z})$ be subsets of size at least $2$ such that $\sum_i T_{i}$ is everything except the $0$ map. Then $t < n-1$ and moreover the bound is sharp.
A general base change construction
We need a way to cook up examples that require no fewer than $n$ Brauer classes to witness an obstruction. We'll accomplish this by first building a conic bundle $\small \tilde{X} \xrightarrow{\tilde{\pi}} \mathbb{P}^1$ that has some desirable properties and then pulling back by a carefully constructed $\small g \colon \mathbb{P^1} \to \mathbb{P^1}$
Tension
Want to construct a conic bundle $X = X_{a,f} : \small y^2 - az^2 = f(x)$ with
- $\small B \cong \text{Br} \, X / \text{Br}_0 \, X$ generated by $n$ quaternion algebras, $\small B = \langle \alpha_1, \dots, \alpha_n \rangle$,
- $X(\mathbb{A}_k) \ne \emptyset$,
- $X(k) = \emptyset$, and in particular $X$ has a Brauer-Manin obstruction that cannot be achieved with any proper subgroup of $B$, so that image of $X(\mathbb{A}_k)$ in $\text{Hom}(B,\mathbb{Q}/\mathbb{Z})$ is everything but the $0$ map.
The number of irreducible factors of $f$ (and their degrees controls) $n$. Getting the other properties simultaneously is like playing Whac-A-Mole.
Starting conic bundle
To accomplish our goals, we start with a conic bundle $\widetilde{X} = \widetilde{X}_{a,\tilde{f}}$ where we force finer control at a finite set of non-archimedean places at the cost of having a rational point on the fiber over $\infty$ in $\mathbb{P}^1$.
We'll ensure $\widetilde{X}$ has $n$ linearly independent Brauer classes which generate $B$ and a finite set of non-archimedean places at which the map $\widetilde{X}(k_v) \to \text{Hom}(B, \mathbb{Q}/\mathbb{Z})$ is surjective.
Starting data
Take $\small n+1$ monic irreducible polynomials $\small \tilde{f}_j$ of even degree and let $\small \tilde{f} = \prod_{j=0}^n \tilde{f}_j$. Both the choice of $a \in k^\times\! \setminus\! k^{\times 2}$ and the finitely many places depend on $\tilde{f}$.
Theorem (BPPSTVV)
Given $\small n,r \in \mathbb{Z}_{>0}$, there is a collection of nonarchimedean places $\small v_0, \dots, v_r$ of $k$ not lying over $2$, a minimal conic bundle $\small \tilde{\pi} \colon \widetilde{X} \to \mathbb{P}^1$, and a collection of Brauer classes $\small \alpha_1, \dots, \alpha_n \in (\text{Br}\, \widetilde{X})[2]$ such that
- The subgroup $\tilde{B} = \langle \alpha_1, \dots, \alpha_n \rangle$ generates $\text{Br}\, \widetilde{X}/ \text{Br}_0 \, \widetilde{X}$
- For each $v_i$, the map $\phi_{v_i} \colon \widetilde{X}(k_{v_i}) \to \text{Hom}(\tilde{B}, \mathbb{Q}/\mathbb{Z})$ is surjective
- For all places $w$, the image of $\phi_w$ contains $0$
To build the conic bundle $X$ that actually has an obstruction, we'll need to keep track of $\small v_0, \dots, v_r$ and the finitely many additional places $v$ where $\phi_v$ is not constant.
A base change
We want to construct a $\small g \colon \mathbb{P}^1 \to \mathbb{P}^1$ so that the base change $\small X := \widetilde{X} \times_g \mathbb{P}^1$ has a Brauer-Manin obstruction.
$$ \begin{CD} X @> >> \widetilde{X} \\ @V{\pi}VV @VV{\tilde{\pi}}V \\ \mathbb{P}^1 @>{g}>> \mathbb{P}^1 \end{CD} $$
To achieve our combinatorial requirements and preserve the structure of the Brauer group after base change, we'll construct $g$ so that it satisfies local conditions at the places $\small v_0, \dots, v_r$ and finitely many additional places $\small w \ne v_i$
Theorem (BPPSTVV)
Let $\small n \ge 1$ and $\small r \ge 0$ be integers. Suppose we can abstractly solve our combinatoral problem , i.e. suppose there exists subsets $\small T_0, \dots, T_r$ of $\small \text{Hom}((\mathbb{Z}/2\mathbb{Z})^n, \mathbb{Q}/\mathbb{Z})$ such that $\small 0 \in T_i$ for all $i>0$ and with
$\small \sum_i T_i = \text{Hom}((\mathbb{Z}/2\mathbb{Z})^n, \mathbb{Q}/\mathbb{Z}) \setminus\{0 \}$.
Then there exist places $\small v_0, \dots, v_r$ of $k$, a conic bundle $X = X_{a,f}$ over $k$, and $B \subset \text{Br}\,X$ with $B \cong(\mathbb{Z}/2\mathbb{Z})^n$ such that
- $B \cong \text{Br}\,X/\text{Br}_0\,X$.
- For each place $v_i$, the image of $X(k_{v_i}) \to \text{Hom}( B, \mathbb{Q}/\mathbb{Z})$ is $T_i$
- For all places $v \ne v_i$ the map $X(k_v) \to \text{Hom}(B,\mathbb{Q}/\mathbb{Z})$ is identically $0$.
In particular $X(\mathbb{A}_k)^B = \emptyset$ and no proper subgroup of $B$ gives an obstruction.
Use the surjectivity
Find subsets $\small T _0, \dots, T_r \subset \text{Hom}((\mathbb{Z}/2\mathbb{Z})^n, \mathbb{Q}/\mathbb{Z})$ such that $\small 0 \in T_i$ for all $i >0 $ and $\small \sum_i T_i = \text{Hom}((\mathbb{Z}/2\mathbb{Z})^n, \mathbb{Q}/\mathbb{Z}) \setminus\{0 \}$.
Fix an isomorphism $\tilde{B} \to (\mathbb{Z}/2\mathbb{Z})^n.$ Since we have places $\small v_0, \dots, v_r$ where the image of $\phi_{v_i} \colon \small \widetilde{X}(k_v) \to \text{Hom}(\tilde{B}, \mathbb{Q}/\mathbb{Z})$ is either surjective or has size at least $2$ and contains $0$, identify $T_i$ as subsets of $\text{im}\, \phi_{v_i}$.
Use the surjectivity
Impose local conditions
First, for each of $\small v_0, \dots, v_r$ control the image of $\small g(\mathbb{P}^1(k_{v_i}))$.
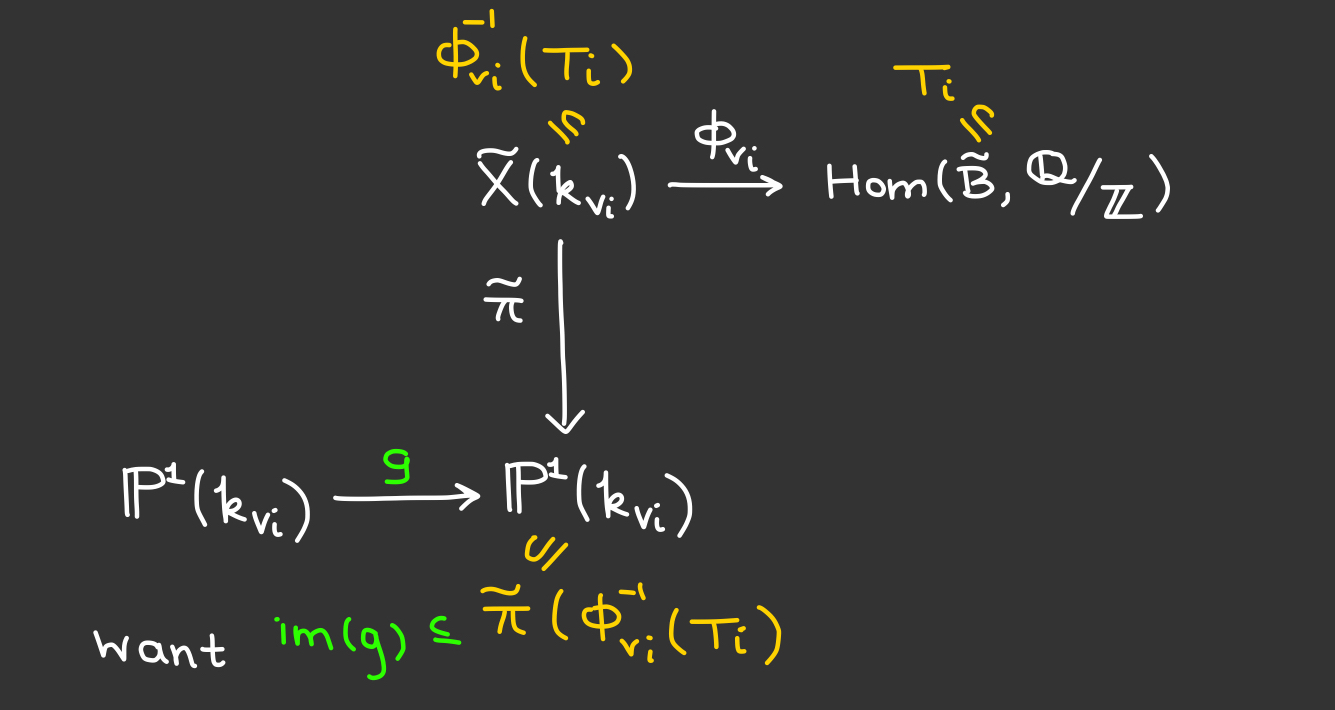
This will help ensure the image of $\phi_{v_i} \colon X(k_{v_i}) \to \text{Hom}((\mathbb{Z}/2\mathbb{Z})^n, \mathbb{Q}/\mathbb{Z})$ is $T_i$.
Impose local conditions
For each $w$ so that $\widetilde{X}_\infty(k_w) = \emptyset$, impose a local condition that will allow us to ensure the image of $\small \phi_w \colon X(k_w) \to \text{Hom}((\mathbb{Z}/2\mathbb{Z})^n, \mathbb{Q}/\mathbb{Z})$ is only the $0$ map.
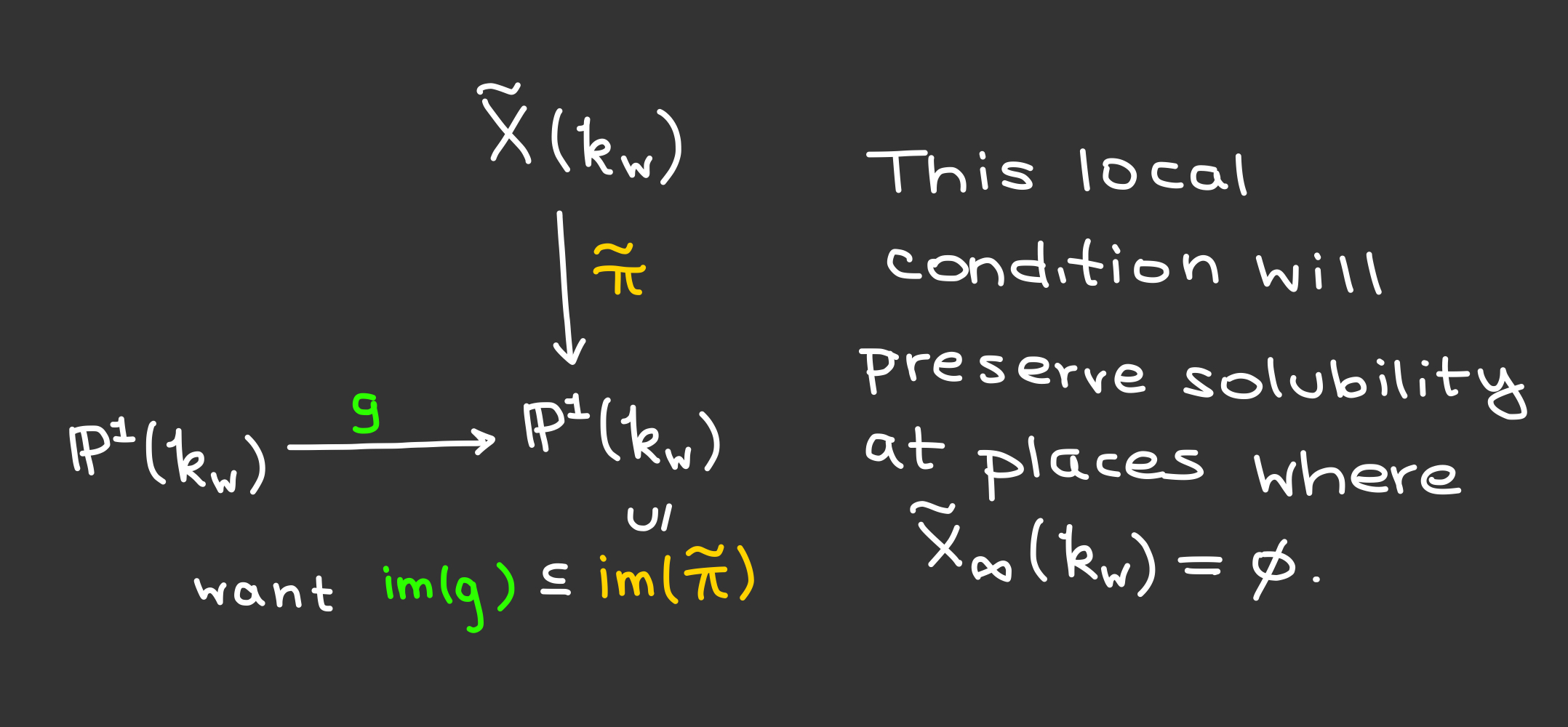
Impose local conditions
We also need to ensure that when we base change, we preserve the Brauer group. That is, the Brauer group of our starting conic bundle $\widetilde{X}$ was generated by quaternion algebras $\tilde{B} = \langle \alpha_1, \dots, \alpha_n \rangle$ with $\tilde{B} \cong \text{Br}\, \widetilde{X}/ \text{Br}_0 \, \widetilde{X}$.
We want the pullback of this subgroup to $\text{Br}\ X$ to be isomorphic to $\text{Br}\,X /\text{Br}_0\,X.$
We do this by imposing local conditions on $g$ for finitely many places (disjoint from those previously mentioned) related to the degeneracy locus of $\tilde{\pi}$.
The starting conic bundle
Time permitting
Starting conic bundle
To accomplish our goals, we started with a conic bundle $\widetilde{X} = \widetilde{X}_{a,f}$ where we forced finer control at a finite set of non-archimedean places at the cost of having a rational point on the fiber over $\infty$ in $\mathbb{P}^1$.
We claimed $\widetilde{X}$ has $n$ linearly independent Brauer classes which generate $B$ and a finite set of non-archimedean places at which the map $\widetilde{X}(k_v) \to \text{Hom}(B, \mathbb{Q}/\mathbb{Z})$ is surjective.
Starting data
Take $\small n+1$ monic irreducible polynomials $\small \tilde{f}_j$ of even degree and let $\small \tilde{f} = \prod_{j=0}^n \tilde{f}_j$
Forcing surjectivity
We pick the non-archimedean places $\small v_0, \dots, v_r$ and $\small a \in k^\times \!\setminus\! k^{\times 2}$ based on $\small \tilde{f}$, and pick $a$ so that $v_i(a) = 1$ for all $i$. We have the quaternion algebras $\small \alpha_j = (a, \tilde{f}_j)$ for $1 \le j \le n$.
Given $\small x_{v_i} \in X(k_{v_i})$, detecting whether $ \small \langle \alpha_j, x_{v_i} \rangle = 0 \text{ or } \frac{1}{2}$ in $\small \mathbb{Q}/\mathbb{Z}\,$ essentially amounts to knowing whether the image of $f_j(\pi(x_v))$ in the residue field $\mathbb{F}_{v_i}$ is a square or not. So this is what we control.
It's hip to be a square (A proposition)
Let $\small \mathbb{F}$ be a finite field. Let $\small f_0, \dots, f_n \in \mathbb{F}(x)$ and $\small d := \sum \text{deg} f_j$. Assume the $f_j$ are independent in $\small \mathbb{F}(x)^\times/\mathbb{F}(x)^{\times 2}$.
If $\small \#\mathbb{F}$ is sufficiently large relative to $n$ and $d$, then for any choice of $\small \varepsilon_0, \dots, \varepsilon_n \in \mathbb{F}^\times$, there exists $c \in \mathbb{F}$ such that $f_j(c) \varepsilon_j \in \mathbb{F}^{\times 2}$ for all $i$.
The idea
For the place $v_i$, surjectivity of $\phi_{v_i}$ means realizing all $2^n$ tuples of values from the Brauer-Manin pairing from points $x_{v_i} \in X(k_{v_i})$ with the $\alpha_j = (a, \tilde{f}_j)$ .
Choose any $\small \varepsilon_1, \dots, \varepsilon_n \in \mathbb{F}_{v_i}^\times/\mathbb{F}_{v_i}^{\times 2}$ and set $\small \varepsilon_0 = \varepsilon_1 \varepsilon_2 \cdots \varepsilon_n.\,$ Apply our proposition to get a $\small c \in \mathbb{F}_{v_i}^\times$ such that $\small \tilde{f}_j(c) \varepsilon_j \in \mathbb{F}_{v_i}^{\times 2}.$ Now, whether $\tilde{f_j}(c)$ is a square is determined by whether $\varepsilon_j$ is a square!
An explicit example over $\mathbb{Q}$
A related base change approach
To construct an explicit example over $\mathbb{Q}$, we build a conic bundle $X_{p,f}$ arising as a base change of a conic bundle $\widetilde{X}_{p, \tilde{f}}$ by a map $g \colon \mathbb{P}^1 \to \mathbb{P}^1$.
Will not perfectly fit into the previous framework, but does have several desirable properties and similarities.
Starting data
Two primes $p$ and $q$. We'll require $p \equiv 1 \bmod{8}, \,$ $p \not \equiv \square \bmod q$, but $p$ is a square modulo small primes (determined by $n$ and $q$).
Features
- Leading coefficient of $f$ is the prime $q$; ensures $X_{\infty}(\mathbb{Q}) = \emptyset$.
- Irreducible factors $\tilde{f}_i$ of $\tilde{f}$ are linear (odd degree). This comes at a cost: now $\text{Br}\,\widetilde{X}/ \text{Br}_0 \,\widetilde{X}$ has a more complicated description and $2$-rank $< n$
- $g$ is constructed as a polynomial of degree $p+1$ and so that the image of $X(\mathbb{Q}_p) \xrightarrow{\phi_p} \text{Hom}(B,\mathbb{Q}/\mathbb{Z})$ is everything but the $0$ map, while $\text{im} \, \phi_v = \{0 \} $ for all other primes $v$.
Explicit computations
| $n$ | \( q \) | \( p \) |
| \( 3\) | \( 5\) | \( 193\) |
| \( 4\) | \( 5\) | \( 1873\) |
| \( 5\) | \( 7\) | \( 55201\) |
| \( 6\) | \( 7\) | \( 107449\) |
| \( 7\) | \( 11\) | \( 30431209\) |
This means, when $n=4$ our conic bundle $\small X_{p,f}$ has $\small \deg(f) = (1873+1)^5 = 23112553675790624$.